Intro

My attempts to improve my results with the small amount of data I’ve collected from the DIYRobotCar race track. So far I have fourteen thousand samples collected by manually driving clockwise around the track. Since my web app based controls are hard to use, there are far more ‘stop’ commands than anything else, making, I think, for very messy training data. Which seems to be reflected in the poor validation accuracy. That remains to be tested.

For now I’ve varied both the shape of the network and the training hyperparameters to see if I can improve things.

Each plot represents the mean and standard deviation of five runs that are identical except for random weigth initialization and choice of batches.

Methods and Results

This is very similar to the network used by the current DonkeyCar code.

Model:

Input image shape: 120x120x3
Dropout 1
Convolution, 24 5x5 filters, stride 2
Convolution, 32 5x5 filters, stride 2
Dropout 2
Convolution, 64 5x5 filters, stride 2
Dropout 3
Convolution, 64 3x3 filters, stride 2
Convolution, 64 3x3 filters, stride 1
Dropout 4
Fully Connected, 100 nodes
Dropout 5
Fully Connected, 50 nodes
Fully Connected (output layer), 5 nodes, softmax activation

All convolution and fully connected layers use relu activation, unless stated otherwise, and all of them use the same L2 regularization hyperparameter.

I handle dropout layers a bit differently than DonkeyCar does. For my original model I started with a list of five dropout values that gets passed to the model making function, so I’ve carried that over to this model rather than rewriting all of my code. The default batch size is small because it was also being used for my tests with RNN layers, where the combination of batch size and number of timesteps can’t be too large.

Default Hyperparameters:

l2_reg: 0.005
dropouts: [0.2,0.2,0.2,0.2,0.2]
learning_rate: 0.003
batch_size: 5
optimizer: RMSprop
validation_split: 0.20

All experiments except the first report validation accuracies for all five runs. The reported value is the max of the running mean within a training run, with a window of five samples.

Experiment One

Experiment Two

The only change here was to merge the two fully connected layers to a single larger layer. So that part of the network looks like:

Dropout 4
Fully Connected, 256 nodes
Dropout 5
Output layer

vals: [0.5193605714115326, 0.5193605714115326, 0.5193605714115326, 0.5193605714115326, 0.569520431677571]

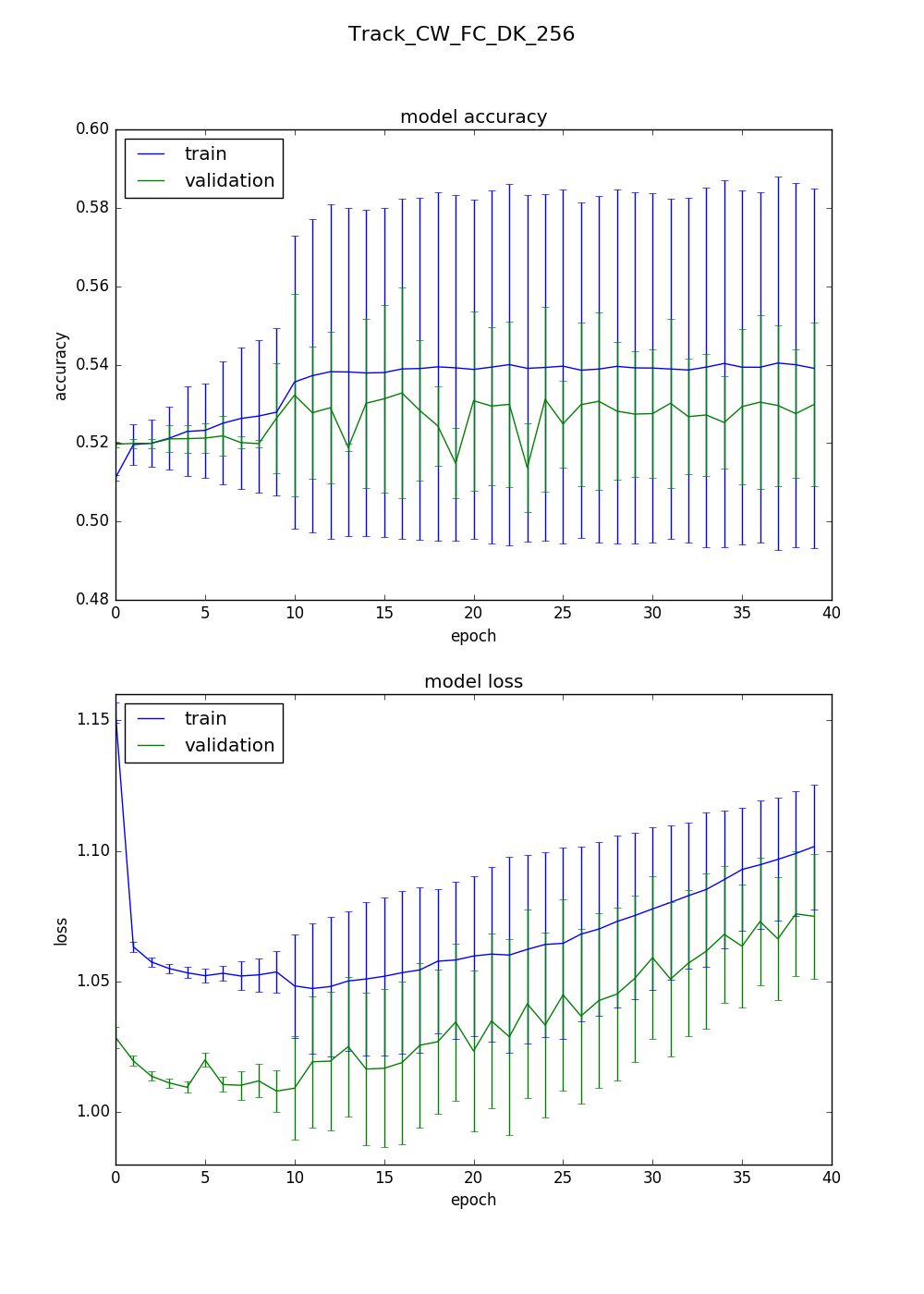
Experiment Three

For the rest of the experiments I used hyperopt to try to find better hyperparameters.

The testing ‘space’ I used was:

space = { 'learning_rate': hp.loguniform('learning_rate', -9, -4 ),
          'l2_reg': hp.loguniform('l2_reg', -10, -3 ),
          'batch_size': hp.quniform('batch_size', 5, max_batch, 1),
          'dropouts': hp.choice('dropouts', ["low","mid","high","up","down"]),
          'optimizer': hp.choice('optimizer', ["RMSProp", "Adagrad", "Adadelta", "Adam"]) }

For the dropout hyperparameter I use this code to convert from the categorical values to dropout layer probability:

    if dropouts == "low":
        dropouts = [0.2,0.2,0.2,0.2,0.2]
    elif dropouts == "mid":
        dropouts = [0.4,0.4,0.4,0.4,0.4]
    elif dropouts == "high":
        dropouts = [0.6,0.6,0.6,0.6,0.6]
    elif dropouts == "up":
        dropouts = [0.2,0.3,0.4,0.5,0.6]
    elif dropouts == "down":
        dropouts = [0.6,0.5,0.4,0.3,0.2]

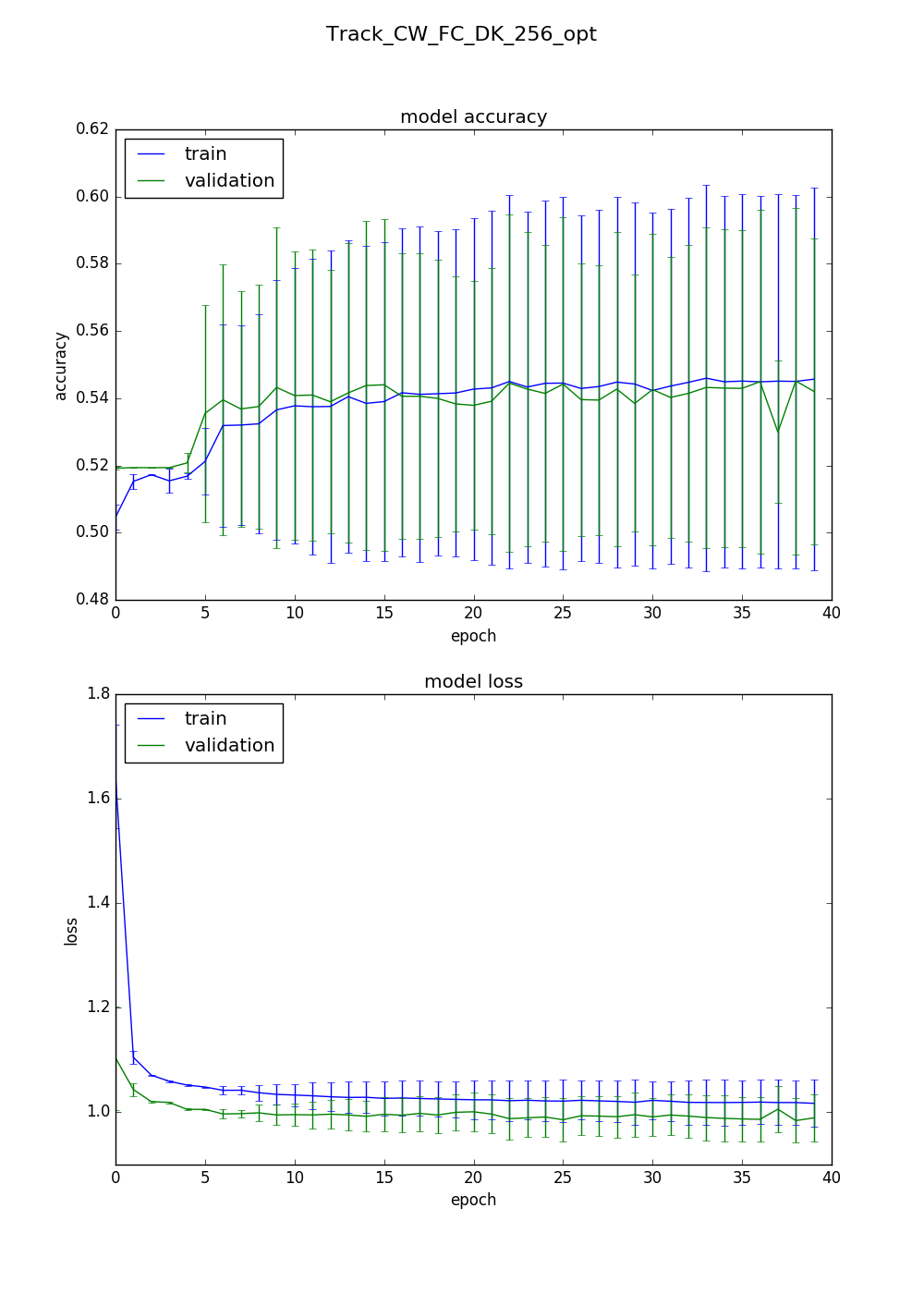
The best validation accuracy achieved after 100 hyperopt trials was with these hyperparameters:

l2_reg: 0.00248097383585
dropouts: [0.2, 0.3, 0.4, 0.5, 0.6]
learning_rate: 0.00315905724545
batch_size: 65
optimizer: Adam

Validation accuracies: [0.6381527690438564, 0.5193605824550663, 0.5193605824550663, 0.5193605824550663, 0.5193605824550663]

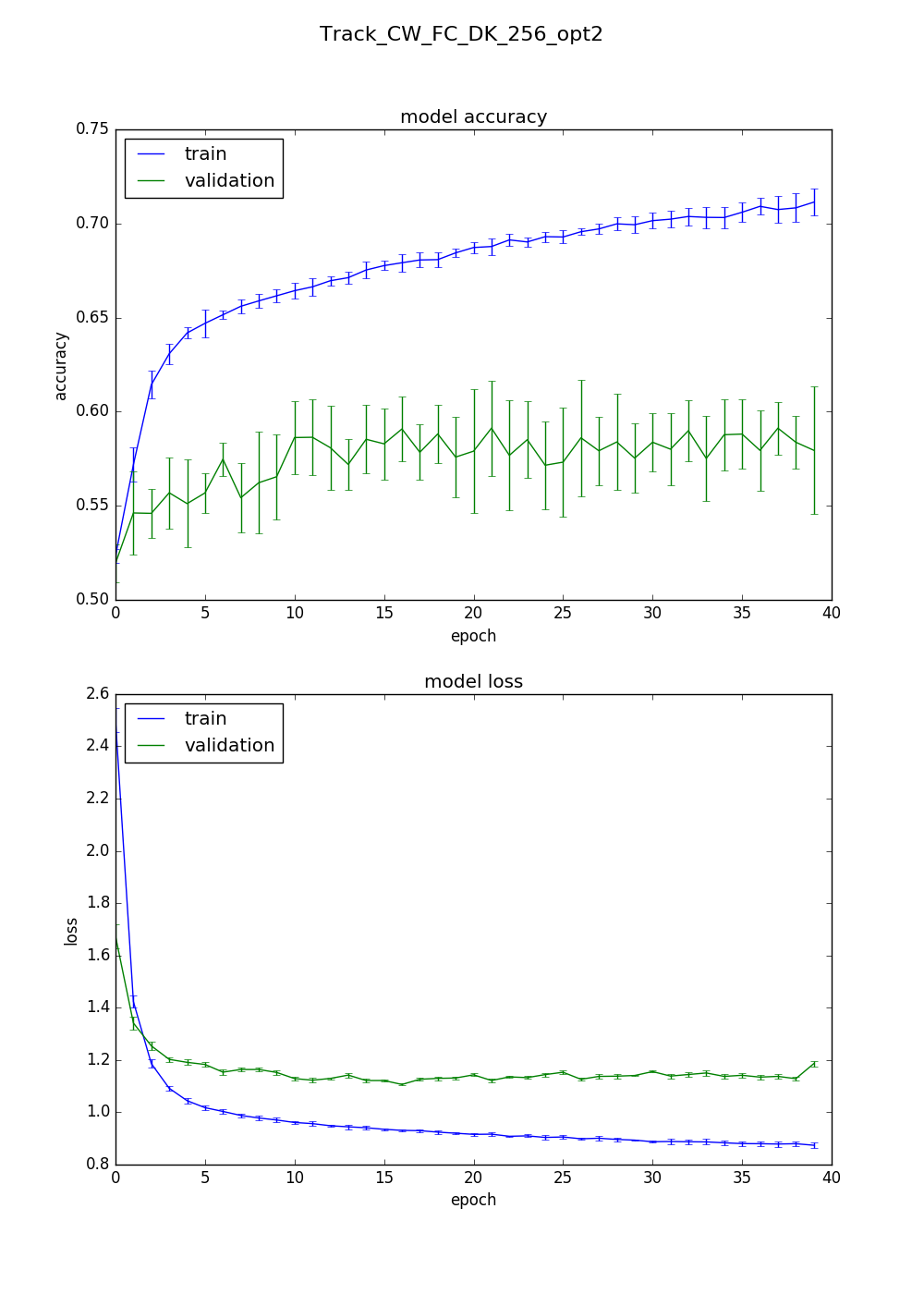
The second best accuracy was with:

l2_reg: 0.00115070702991
dropouts: [0.2, 0.3, 0.4, 0.5, 0.6]
learning_rate: 0.000648285497249
batch_size: 71
optimizer: Adam

Validation accuracies: [0.5749911179762751, 0.6154174035014734, 0.5796802829912671, 0.6100177615023422, 0.5947424494754358]

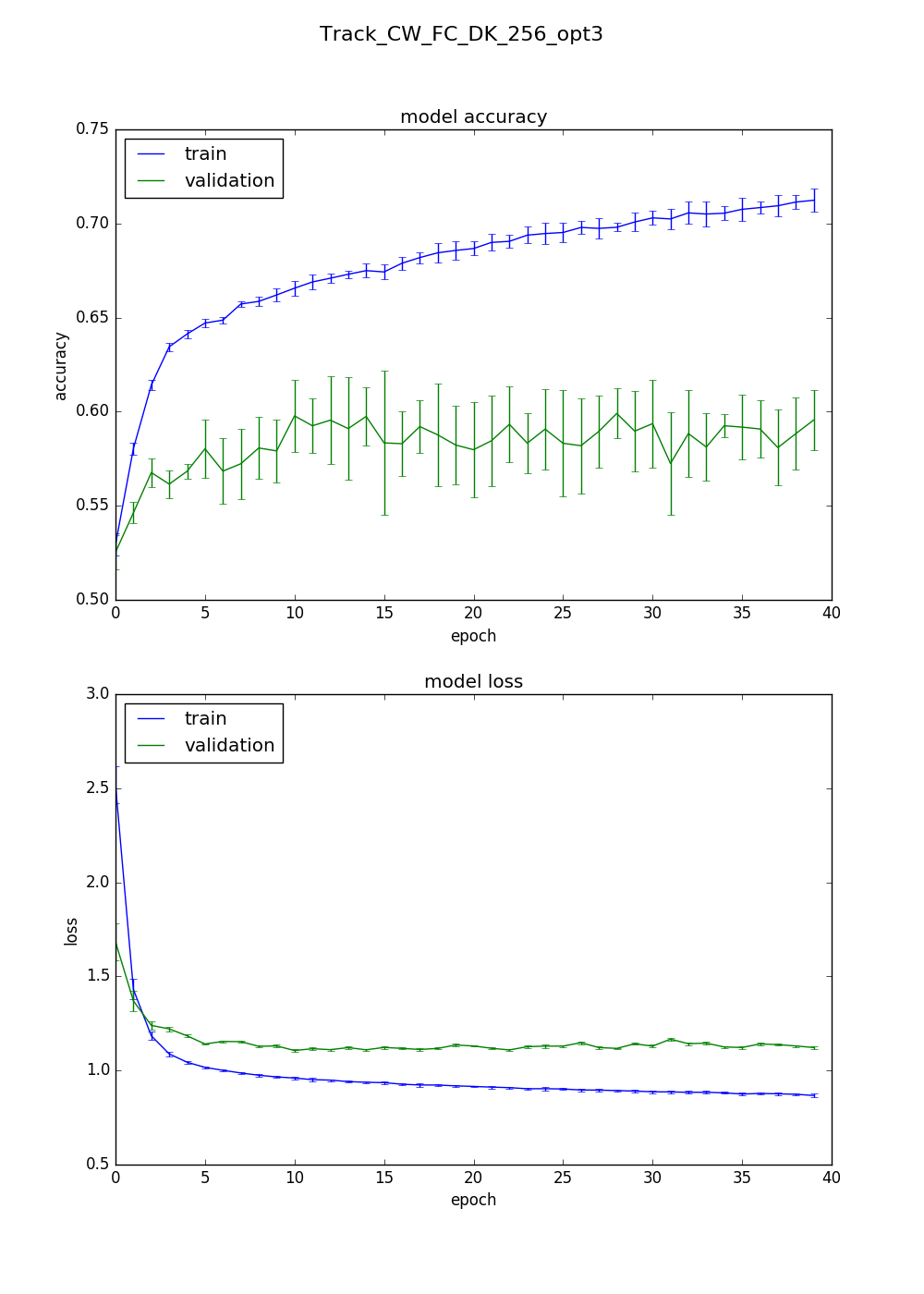
Third best:

l2_reg: 0.00741098464201
dropouts: [0.2, 0.3, 0.4, 0.5, 0.6]
learning_rate: 0.000589721466932
batch_size: 60
optimizer: Adam

Validation accuracies: [0.5972291300923532, 0.6239431615091768, 0.6136412062716949, 0.5841563050107464, 0.5814564846442818]

Last but not least. A plot of all one hundred hyperplot runs versus validation accuracy. There’s clearly some improvement going on, which suggests that hyperopt is doing better than just random or grid search. Equally as clearly, the absolute improvement is pretty small, Maybe from 0.52 to 0.55 or 0.56 at best. To me that suggests there are more fundamental issues with my training than un-optimized hyperparameters.

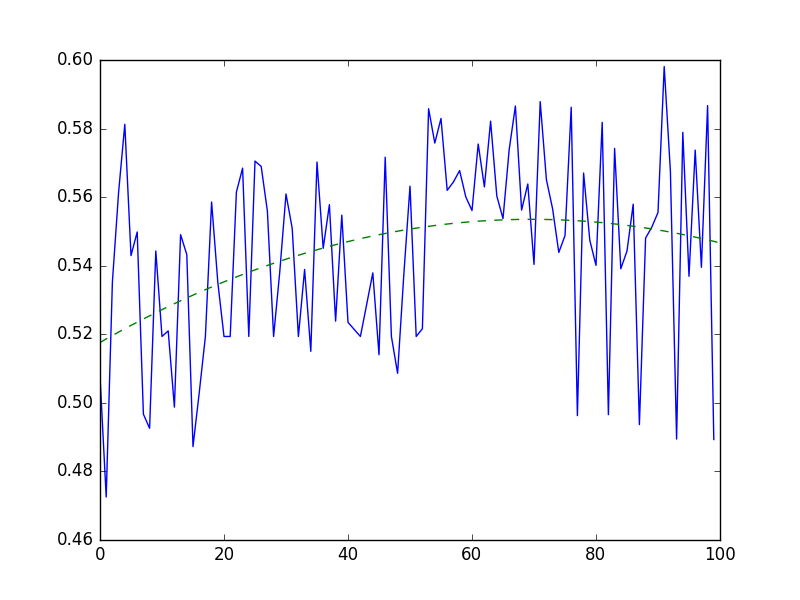
Conclusions

Mostly this leaves me with more questions than answers. The first experiment doesn’t make sense at all and I should probably re-run it with a more reasonable batch size. The second one is a bit more reasonable but there’s so much variation from run to run that it’s hard to say. Probably also ought to be repeated with a larger batch size.

The ‘best’ set of hyperparameters found did use a larger batch size, but there’s still a huge amount of variation. The learning rate on this one is ten times higher than the next two, which could be an issue.

The last two look more reasonable even if the training and validation accuracies are still a lot lower than I would hope for.

Future

• Plot each hyperparameter against the validation accuracy to see if there are any obvious trends.
  • I had a quick look at this and batch size, learning rate and L2 regularization all show very faint curves with peaks about where hyperopt found then. I could almost certainly narrow the search spaces the next time I do this.
• Try again with skopt (SciKit Learn’s optimization module).
• Repeat all of the above with RNN layers?
• Clean up the data with my dagger tool, retesting after each quarter of the data, maybe?

Version

Updated Feb 7, 2018 with the hyperopt plot and some details about individual hyperparameters.